How to Teach Your Child Math

You can stand on the shoulders of an American Giant... for free.

Mar 22, 2021

Ray's Arithmetic is your one-stop shop for math at all levels covering all major concepts. Joseph Ray, contemporary of Abraham Lincoln and a math professor at a private preparatory academy in Ohio, taught math like a BOSS for 25 years. From the description: "Ray [...] had no use for indolence and sham. He was always delighted to join his students in sports. He knew how to use balls, marbles, and tops as concrete illustration to help young children make the transfer from solid objects to abstract figures.

"From the Presidency of Abraham Lincoln to that of Teddy Roosevelt few Americans went to school or were taught at home without considerable exposure to either Ray's Arithmetic or McGuffey's Readers - usually both. Ray and McGuffey challenged students to excellent accomplishment. Their influence o n our country has certainly eclipsed Mann's and rivaled Dewey's, but education histories, edited by humanists, seldom mention these men.

"Ray's classic Arithmetics are now brought to a new generation which is in. search of excellence."

I own physical copies of Ray's Arithmetic; they are peerless. Sequential, organized, with plenty of practice for learners at all levels. They're also charming; multiplication problems in the book are reminiscent of episodes of Little House on the Prairie or the books in the Anne of Green Gables series.

Ray knew his stuff, but he was also, no doubt, a hard-ass. This book is old school. It's logical, thorough, and no-nonsense, which is why it works. If your kid can stick with Ray, she will be more numerate (math literate) than the average 18-year-old high school graduate.

WAY MORE.

If you have a future engineer, scientist, coder, mathematician or doctor on your hands, use Ray's Arithmetic and she'll be well ahead of the curve well before she hits high school.

Having said that, Ray requires grit.

Here's why.

In the excellent book, A Mind for Numbers, Barbara Oakley explains just what it takes to learn anything complicated, such as math. Her work builds on the same studies as Daniel Coyle's discussion of the development of young athletes in The Talent Code and in Geoff Colvin's excellent treatise, Talent is Overrated both of which blow apart the idea that talent is innate and unreproducible in those who are not born with strong initial skill in a discipline.

The skinny is that the most susccesful students (or athletes) improve their skillset through deliberate practice. James Clear, the author of Atomic Habits defines this idea for us: "While regular practice might include mindless repetitions, deliberate practice requires focused attention and is conducted with the specific goal of improving performance."

What Ray does magnificently is provide different versions of the same type of problem. He always begins simply, with lists of problems like the ones you remember from your old math textbooks. This repetition is necessary. Many schools are trying to move away from drill and kill at younger ages to focus on theory and multiple methods of problem-solving. Developmentally, this is not an appropriate response for young learners, who need significant meaningful practice to memorize combinations of numbers 1-20 and their multiplication tables in order to have the bank of knowledge which makes solving harder problems easier. In his Introduction to Mathematics, Alfred North Whitehead states: "It is a profoundly erroneous truism repeated by all copybooks, and by eminent people when they are making speeches, that we should cultivate the habit of thinking of what we are doing. The precise opposite is the case. Civilization advances by extending the number of operations which we can perform without thinking about them. Operations of thought are like cavalry charges in battle - they are strictly limited in number, they require fresh horses, and must only be made at decisive moments."

Ray begins his work clearly understanding this premise. When introducing anything new, you start easy and repeat, repeat, repeat. Kid feels successful, is able to move faster, gains confidence.

Level up.

Kid proceeds more slowly, making connections to the previous work, but she already has the skills necessary to complete the next skill. She repeats, repeats, repeats, gains confidence, gains speed, levels up.

This process of repetition with different versions of a similar type of problem helps the student to internalize the processes necessary to develop increasingly difficult math skills.

Then Ray gets really good. I'm a neuroscience hobbyist. The repetition of one type of problem transfers the single problem from short-term memory into long-term memory, because the brain recognizes the process as something important to know because the kid keeps doing it. Human brains are very efficient survival machines. If the brain senses that a particular operation must be repeated with frequency, it will chunk the individual steps of solving a problem, combining them into one solid piece of knowledge that's more quickly and easily recalled. Think of brushing your teeth. When you decide you're tired of morning coffee breath, you decide to brush your teeth. But you don't think, "First I'll walk to the bathroom. Then I'll put my hand on the doorknob. Then I'll turn the knob and push open the door. Then I'll walk to the sink. Then I'll grab the toothpaste. Then I'll unscrew the cap. Then I'll get my toothbrush. Then I'll squeeze a dollop of toothpaste on top of my toothbrush. Then I'll put the toothbrush in my mouth..." etc., etc. Nope, instead you think, "Time to brush my teeth." And you do it without thinking about the steps.

In the rush to make the classroom more child-centered and honor all the ways a child can learn to do math, we've forgotten how best to activate the human brain into survival-optimization mode and force it to repeat, repeat, repeat similar problems, then level up, then keep doing that until we can peruse a Calculus textbook without being overcome by nausea. Instead, we skimp on practice now and spend most of our time discussing different ways to attack one problem. Bottom line: our quickly falling National Education Progress (NAEP) scores in math demonstrate how poorly the newer approaches work. My gifted seniors rely on calculators for basic arithmetic calculations. How many people in our country would shy away from onerous loan terms and unaffordable debt loads if they could run a percentage in their heads?

Your kids can do better, be better, because you have Ray on your side.

Once the basic skill is learned, Ray introduces focused practice in the form of word problems. He must have observed that students needed a different context to practice in. He recognized their need to take the solution processes they had chunked in earlier repetitions and pull them apart in order to figure out how to solve a problem presented in a different way. In order to do this, Ray designed word problems to give students a story context that makes the problem real to them. Emotion drives memory. If you can make students feel something about their work, especially if part of it is recognizing the survival-optimization value of being able to do math quickly and accurately, then the brain is, again, more likely to move mathematical operations into long-term memory.

I will admit there have been times when Ray has stumped me when one of my children was working in his books and asked for help, but the end result was that... I became better at math too. (Good teachers are tricksy hobbitses.)

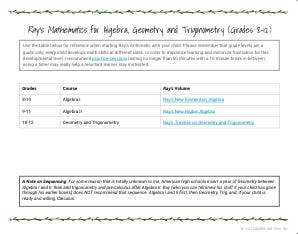
Below this post are much of Ray's work, including links to PDF versions of his books and answer keys for grades K-8. (I've included Ray's Algebra I and II as well as Geometry and Trigonometry, but I don't have the keys for those volumes, so your mileage may vary.)

I put the recommended grade level besides each book, but these are not hard and fast categories. If your 4th grader needs to start at the beginning of Ray's Primary Math, don't rail at her. Put your fist into the sky and celebrate that she has access to one of the best math teachers America ever produced. (If you want to get angry because you thought your child's grades in math reflected her actual ability, be mad at the school system that defrauded your child of a real education. Then pat yourself on the back for giving her one. And if you're still mad after that, prepare to go to the local school board meeting and give them an earful and a copy of Ray's New Primary Arithmetic.)

I recommend getting your child a composition book to record her math progress. If your kid struggles, use the Pomodoro technique. Give her a 15- or 25- minute work period, followed by a 10-15-minute play period. Do not chide her if her progress is slow. Just set a goal together. Completing one lesson a day is fine. Keep in mind that your primary goal is to build her competence and thus, her confidence and grittiness. Keep doing Pomodoros until she finishes the lesson.

Yes, you can use Prodigy or other adaptive math apps, but electronics do more harm than good at a young age. If you default to the computer, understand that you're sacrificing a big benefit of Ray's work: helping students develop grit and confidence.

If your child is (or you are -- if, say, you're a high schooler trying to keep up with school in the absence of actual in-class instruction) struggling with a math concept, you may want to consult Khan Academy which is free. Khan is very good at explaining complex concepts and, more importantly, clearly breaking down the steps so students can pinpoint where they might be going wrong.

And if you are an advanced math learner, one of the most powerful things you can do to show you know a concept if to use Feynman's technique to nail it down fully in your own head (and maybe help a younger sibling/friend in the process.)

Math is a process. Start where you're competent and hold Ray's hand as he leads you down the path toward math competency most high school teachers can only dream of.